Jak działa refraktometr

Refraktometry to urządzenia optyczne do testowania cieczy i ciał stałych, służące do pomiaru kąta załamania światła (kąta refrakcji), czyli stopnia, w jakim światło zmienia kierunek przechodząc przez daną substancję. Może być nią np. roztwór sacharozy lub szkło. Refraktometria jest szeroko stosowaną techniką pomiarową, najczęściej jest jednak wykorzystywana do szybkiego określania stężenia roztworów. Refraktometria cechuje się również wysoką dokładnością, nie jest też techniką skomplikowaną.

Prawo Snella to prawo, które opisuje przechodzenie światła przez dwa sąsiadujące ze sobą ośrodki. Jest również znane jako prawo załamania światła.

n1×sinθ１＝n2×sinθ２

• n1：współczynnik załamania światła przy wejściu do ośrodka
• θ1：kąt padania światła
• n2：współczynnik załamania światła przy wychodzeniu z ośrodka
• θ2：kąt padania światła

Sinus (sin) to kod konwersji służący do oznaczania wysokości trójkąta prostokątnego za pomocą kąta.
Przypadki spacjalne … sin0° = 0, sin30° = 1/2, sin45° = √2/2, sin60° = √3/2, sin90° = 1
Jeżeli θ rośnie, sinθ także rośnie.

Światło padające prostopadłe do powierzchni granicznej ośrodka (0°) porusza się po linii prostej, bez załamania.
Graniczna powierzchnia światła staje się widoczna po stronie ośrodka o wyższym współczynniku załamania światła
Nawet jeśli kierunek padania światła jest odwrócony, światło porusza się po tej samej linii (odwracalność linii światła)

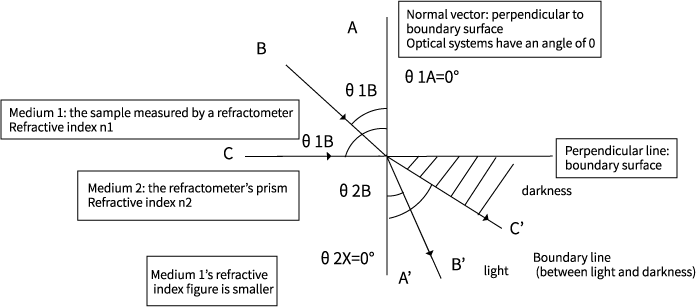
Promień A
Weźmy pod uwagę promień A.

• ｎ１sinθ１A＝ｎ２sinθ２A'
• ｎ１×０＝ｎ２×sinθ２A'
• ０＝ｎ２×sinθ２A'

θ1A wynosi 0, więc niezależnie od wartości n1, wyniesie 0. Aby n2×sinθ2A' było równe 0, θ2A' również musi wynosić 0. Zatem światło wpadające bezpośrednio z góry wyjdzie bezpośrednio poniżej. Światło wektora normalnego wychodzi jako wektor normalny.

Promień B
Weźmy pod uwagę promień B.

ｎ１sinθ１B＝ｎ２sinθ２B'
Biorąc pod uwagę, że n2 jest większe niż n1, sinθ2B' musi być mniejsze niż sinθ1B, w przeciwnym razie obie strony równania nie będą równe. Aby sinθ był mniejszy, θ musi być małe, a θ2B’ będzie mniejszym kątem padania niż θ1B. Ukośne promienie światła, takie jak promień B, załamują się i wpadają do następnego ośrodka.

Promień C
Weźmy pod uwagę promień C.

Promień C jest promieniem światła skierowanym pod kątem 90° od wektora normalnego i znajdującym się na powierzchni granicznej pomiędzy dwoma ośrodkami. Często nie wiadomo, co dzieje się ze światłem na powierzchni granicznej, ale istnieje przynajmniej promień 89,9°. Światło o kącie większym niż 90° (90,000001°) jest światłem z ośrodka 2, zatem jeśli pominiemy to światło, to promień o kącie 90° będzie największym możliwym kątem.

• ｎ１sinθ１C＝ｎ２sinθ２C'
• ｎ１sin90°＝ｎ２sinθ２C'
• ｎ１×１＝ｎ２sinθ２C'
• ｎ１＝ｎ２sinθ２C'

Przy zastosowaniu sin90° = 1 mnożenie przez 1 znika. Lewa strona wzoru staje się po prostu n1.
n2 to współczynnik załamania pryzmatu… który jest już znany.
θ2 to kąt załamania… który wymaga pomiaru n1.
Współczynnik załamania światła można zmierzyć mierząc kąt padania światła pod kątem padania 90° (prostopadle do pryzmatu).
Refraktometry to urządzenie mierzące kąt padania światła i przetwarzające ten kąt na współczynnik załamania światła.